My first-author paper ”The role of spatial embedding in mouse brain networks constructed from diffusion tractography and tracer injections” has been published online at NeuroImage.

I published the analysis and visualization code I developed for this project in a Python package called Braingraphgeo. You can check out the code here!

Highlights

• I constructed structural brain networks using diffusion MRI tractography and public tracer data
• I generated random geometric surrogate networks to use as a baseline for comparative network analysis
• I found that modular- and hub-node structure in tractography networks are heavily biased by geometry

Motivation

Diffusion MRI tractography is the only way to noninvasively measure the structural connectivity of the brain, but recent validation studies have revealed that there are severe limitations in modern approaches.

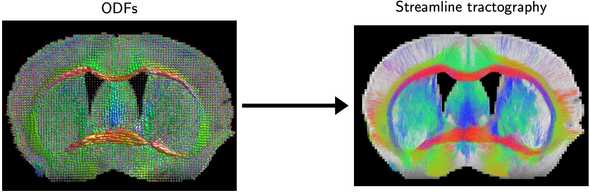
Tractography forms “streamlines” by picking a seed point in 3D space, taking a step in a direction determined by the local fiber orientation distribution function (fODF), sampling a new direction from the new fODF, taking another step, etc. Accordingly, one major problem inherent to the method is that local errors in fiber orientations accumulate over larger distances, so longer streamlines have more errors, causing a bias towards connectivity between nearby structures.

Part of the challenge of detecting this bias is that the brain is itself a spatially-embedded network - there is an actual, biological bias towards short-range connections in addition to the methodological bias imparted by tractography.

The purpose of this project was to use neural tracer data from the Allen Mouse Brain Connectivity Atlas to distinguish these two biases using a number of techniques from graph theory. Neural tracers use fluorescent viruses that infect only specific pathways in the brain based on where they were injected. With optical imaging, you can precisely quantify regions of tracer infection, giving you close to a ground-truth measure of connectivity between different regions.

Strategy

Brain graphs were constructed from six diffusion MRI mouse datasets using streamline tractography. The “nodes” in the graph were the same as those from the tracer graph, defined as specific anatomical brain regions. The “edges” in the tractography graphs were defined as the number of streamlines connecting any two regions, normalized by the size of the two regions.

From these “empirical” graphs, we were inspired by a recent paper to construct geometric surrogate graphs that have the same edge-weight distribution and weight-distance relationships as the empirical graphs, but are otherwise randomly connected.

Using a host of analytical tools from graph theory, comparison between the empirical and geometric surrogate graphs then allows us to quantify the extent to which brain network structure from each modality can be explained by the brain’s geometry alone.

Results

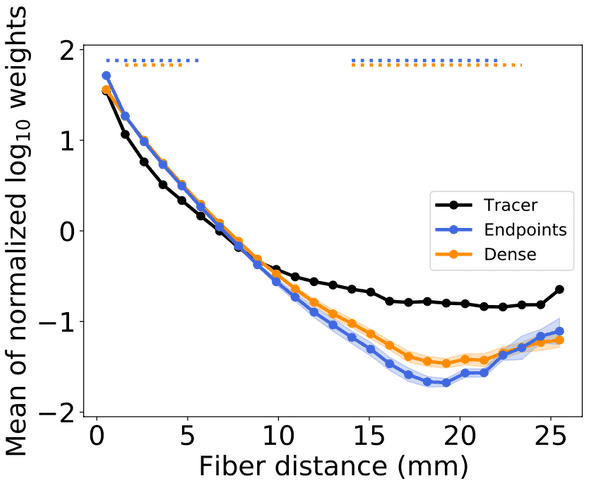
Tractography networks (blue and orange) dramatically underestimate connectivity at long distances relative to tracers:

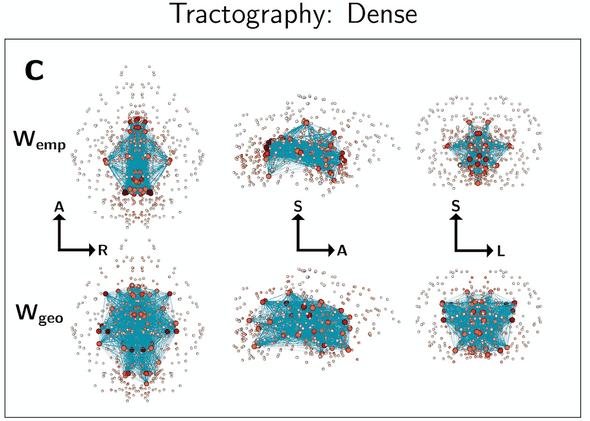
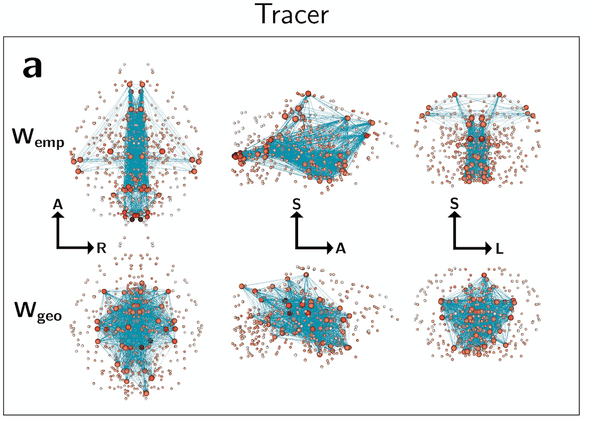
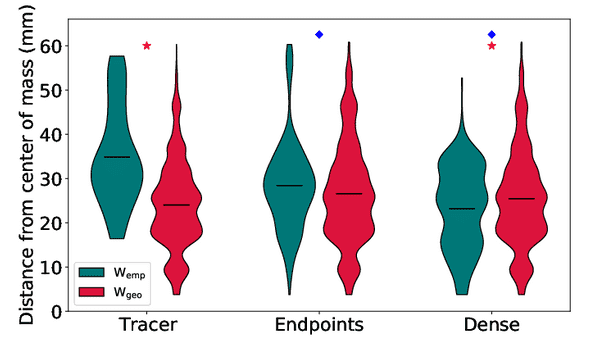
Tractography networks (Wemp) place their most important “hub” nodes towards the center of the brain, similar to their corresponding geometric surrogate graphs (Wgeo):

Tracer networks (Wemp), however, place their most important “hub” nodes further out into the periphery of the brain, which is not observed in their corresponding geometric surrogate graphs (Wgeo):

This effect is quantified below, where we see distributions of the distance from the center of mass of major hub nodes in empirical and geometric graphs from tracers and two tractography methods:

Across many other metrics, we saw a similar story: tractography graphs are not only significantly different than ground-truth tracer graphs, but they are also indistinguishable in many respects from random graphs with the same geometric characteristics. This indicates that geometric bias is still a huge problem in tractography, and demonstrates a useful analytic tool for future benchmarking of new methods.